학습 내용
1. 선형대수란?
- 벡터와 행렬을 사용하여 선형 방정식 시스템을 연구하고 해결하는 수학의 한 분야이다.
- 벡터 공간, 선형 변환, 고유값과 고유벡터, 행렬 연산 등을 다루며, 수학적 모델링과 데이터 분석에 널리 활용된다.
- 머신러닝의 핵심 아이디어가 행렬에 관한 식으로 표현되는 경우가 많기 때문에 탄탄한 기초가 필요하다.
2. 선형대수 기본표기법(Basic Notation)
- A∈R^(m×n) 는 m개의 행과 n개의 열을 가진 행렬을 의미한다.
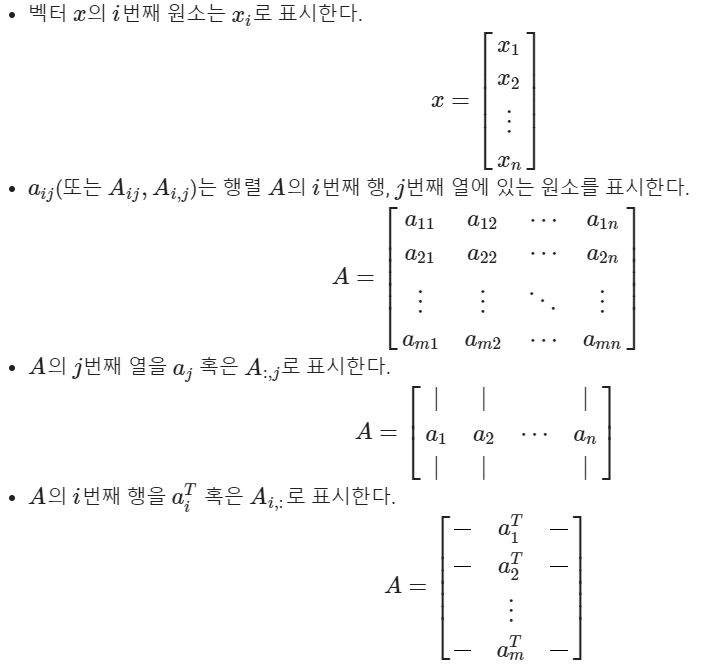
- x∈R^(n)는 n개의 원소를 가진 벡터를 의미한다. n차원 벡터는 n개의 행과 1개의 열을 가진 행렬로 생각할 수도 있다. 이것을 열벡터(column vector)로 부르기도 한다. 만약, 명시적으로 행벡터(row vector)를 표현하고자 한다면, x^T(T는 transpose를 의미)로 쓴다.
- 벡터 x의 i번째 원소는 xi로 표시한다.
3. 행렬의 곱셈
- 벡터X벡터
- 내적 : 점곱(내적)은 두 벡터의 대응하는 성분을 곱한 후, 그 곱셈 결과들을 모두 더하여 계산한다. 예를 들어, 벡터 a^T = (a₁, a₂, ..., aₙ)와 벡터 b = (b₁, b₂, ..., bₙ)의 곱셈은 a₁b₁ + a₂b₂ + ... + aₙbₙ 이다.
- 내적 : np.dot(x,y) => numpy의 dot 사용

- 외적 : 벡터 a = (a₁, a₂, a₃)와 벡터 b^T = (b₁, b₂, b₃)의 곱셈
[ a₁b₁, a₁b₂, a₁b₃ ]
[ a₂b₁, a₂b₂, a₂b₃ ]
[ a₃b₁, a₃b₂, a₃b₃ ]
- 외적 : np.matmul(x,y) => numpy의 matmul 사용

- 행렬X벡터 : 외적 사용(np.matmul(x,y))

- 행렬X행렬 : 외적 사용(np.matmul(x,y))


4. 행렬의 성질
- 정방행렬(square matrix): 행과 열의 개수가 동일하다.(N x N)
- 삼각행렬(triangular matrix)
- 상삼각행렬(upper triangular matrix): 정방행렬이며 주대각선 아래 원소들이 모두 0이다
[ 1, 2, 3 ]
[ 0, 4, 5 ]
[ 0, 0, 6 ]
- 하삼각행렬(lower triangular matrix): 정방행렬이며 주대각선 위 원소들이 모두 0이다
[ 1, 0, 0 ]
[ 2, 4, 0 ]
[ 3, 5, 6 ]
- 대각행렬(diagonal matrix): 정방행렬이며 주대각선 제외 모든 원소가 0이다.
[ 1, 0, 0 ]
[ 0, 2, 0 ]
[ 0, 0, 3 ]
- 대각행렬 생성 : A= np.diag([1,2,3])
- 대각행렬 값 가져오기 : np.diag(A)
- 단위행렬(identity matrix): 대각행렬이며 주대각선 원소들이 모두 1로 표시한다.
[ 1, 0, 0 ]
[ 0, 1, 0 ]
[ 0, 0, 1 ]
- 단위행렬 생성 : A =np.eye(3)
5. 행렬 전치(Transpose)
: 행렬을 전치하는 것은 그 행렬을 뒤집는 것으로 생각할 수 있다. 행렬 A∈R^(m×n) 이 주어졌을 때 그것의 전치행렬은 AT∈R^(n×m) 으로 표시하고 각 원소는 (A^T)ᵢⱼ = Aⱼᵢ
- 행렬전치의 성질
- (A^T)^T=A
- (AB)^T=B^TA^T
- (A+B)^T=A^T+B^T
- 대칭행렬(Symmetic Matrices) : 정방행렬 A 가 AT 와 동일한것
- A=−(A^T) 일 때는 반대칭(anti-symmetric)행렬이라 한다.
- 대칭행렬의 성징
- A*(A^T) 는 항상 대칭행렬이다.
- A+AT는 대칭, A−AT는 반대칭이다.
- A=(A+A^T)/2+(A−A^T)/2
- 정방행렬의 대각합(Trace)
: 정방행렬 A∈R^(n×n) 의 대각합은 tr(A) 로 표시(또는 trA )하고 그 값은 Aᵢᵢ의 합이다.
- 대각합의 성질

6. 선형독립(Linear Independence)이란?
: 벡터들의 집합 {x1,x2,…,xn}⊂R^m 에 속해 있는 어떤 벡터도 나머지 벡터들의 선형조합으로 나타낼 수 없을 때 이 집합을 선형독립(linear independent)이라고 부른다.
- 역으로 어떠한 벡터가 나머지 벡터들의 선형조합으로 나타내질 수 있을 때 이 집합을 (선형)종속(dependent)이라고 부른다.
- Column rank: 열들의 부분집합 중에서 가장 큰 선형독립인 집합의 크기
- Row rank: 행들의 부분집합 중에서 가장 큰 선형독립인 집합의 크기
- 모든 행렬의 column rank와 row rank는 동일하다. 따라서 단순 rank(A) 로 표시한다.
- 선형독립의 성질

7. 역행렬(The Inverse)이란?
: 정방행렬 역행렬 A^(−1) 은 다음을 만족하는 정방행렬.
A^(−1)*A = I = A*A^(−1)
- 역행렬의 성질

8. 행렬의 치역과 영공간
- 치역(range) : A의 모든 열들에 대한 생성(span)이다.
- 영공간(nullspace) : 영공간(nullspace) N(A) 는 A 와 곱해졌을 때 0이 되는 모든 벡터들의 집합이다.
- N(A)*A = {0}
9. 이차형식(Quadratic Forms)
: 정방행렬 A 벡터 x에 대해 x^T*Ax로 나타내는 함수
- 벡터를 정방행렬에 의해 변환하고, 그 결과를 다시 해당 벡터와 내적하여 스칼라 값을 생성한다.
- 대칭 행렬 A의 특성에 따라 양의 정부호, 음의 정부호, 혹은 양수와 음수가 모두 나타날 수 있는데, 이는 고유값 분해를 통해 분석가능하다.


'데브코스' 카테고리의 다른 글
| 데이터 엔지니어링 69일차 TIL (1) | 2024.07.04 |
|---|---|
| 데이터 엔지니어링 68일차 TIL (1) | 2024.07.03 |
| 데이터 엔지니어링 66일차 TIL (0) | 2024.07.02 |
| 데이터 엔지니어링 65일차 TIL (0) | 2024.06.30 |
| 데이터 엔지니어링 64일차 TIL (0) | 2024.06.30 |

